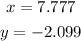• You know that the sum of the two numbers must be:
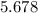
In order to find any pair of numbers whose sum is that number shown above, you can subtract 1 from it:

Now you can set up that:
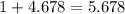
• To find any pair of numbers whose difference is:
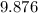
You can add 2 to it:
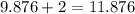
Then, you can set up that:
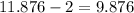
• Let be "x" and "y" the numbers that add up to 5.678. and whose difference is 9.876.
Then, you can set up these equations:
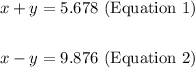
• To solve the riddle, you can follow these steps:
- Set up a System of equations using the equations found in the previous part:
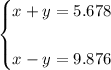
- Apply the Elimination Method by adding both equations and solving for "x":
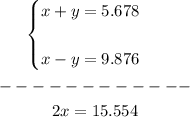

- Substitute the value of "x" into one of the original equations and solve for "y":
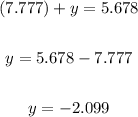
Therefore, the answers are:
• Any pair of numbers whose sum is 5.678:
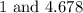
• Any pair of numbers whose difference is 9.876:
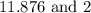
• Equations that represents the riddle:
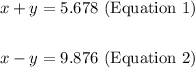
• Solution of the riddle: