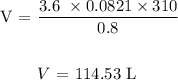Question

A balloon is floating around outside your window. The temperature outside is 37 ∘C , and the air pressure is 0.800 atm . Your neighbor, who released the balloon, tells you that he filled it with 3.60 moles of gas. What is the volume of gas inside this balloon?

Answer 1

`114.53\text{ L}`

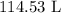
Step-by-step explanation:

Here, we want to get the volume of the gas inside the balloon

Mathematically, from the ideal gas equation:

`\begin{gathered} PV\text{ = nRT} \\ V\text{ = }(nRT)/(P) \end{gathered}`

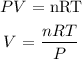
where:

P is the pressure which is given as 0.8 atm

V is the volume which we want to calculate

R is the molar gas constant which is 0.0821 L.atm/mol.K

T is the temperature in Celsius which we can convert to K by adding 273 (273 + 37 = 310 K)

n is the number of moles which is 3.6

Substituting the values, we have it that:

`\begin{gathered} \text{ V = }\frac{3.6\text{ }*0.0821*310}{0.8} \\ \\ V\text{ = 114.53 L} \end{gathered}`