Question

The vertices of two rectangles are A(−5,−1),B(−1,−1),C(−1,−4),D(−5,−4) and W(1,6),X(7,6),Y(7,−2),Z(1,−2). Compare the perimeters and the areas of the rectangles. Are the rectangles similar? Explain.Perimeter of ABCD: , Area of ABCD: Perimeter of WXYZ: , Area of WXYZ:

Answer 1

In order to compare the perimeters and areas, let's first find two adjacent sides of each rectangle.

From ABCD, let's calculate AB and BC:

A and B have the same y-coordinate, so the length is the difference in x-coordinate:

AB = -1 - (-5) = -1 + 5 = 4

B and C have the same x-coordinate, so the length is the difference in y-coordinate:

AB = -1 - (-4) = -1 + 4 = 3

Therefore the perimeter and area are:

`\begin{gathered} P=4+3+4+3=14 \\ A=4\cdot3=12 \end{gathered}`

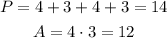
Now, for rectangle WXYZ, let's use WX and XY:

W and X have the same y-coordinate, so the length is the difference in x-coordinate:

WX = 7 - 1 = 6

X and Y have the same x-coordinate, so the length is the difference in y-coordinate:

XY = 6 - (-2) = 6 + 2 = 8

So the perimeter and area are:

`\begin{gathered} P=6+8+6+8=28 \\ A=6\cdot8=48 \end{gathered}`

In order to check if the rectangles are similar, let's check the following relation:

`((P_1)/(P_2))^2=(A_1)/(A_2)`

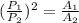
So we have:

`\begin{gathered} ((14)/(28))^2=(12)/(48) \\ ((1)/(2))^2=(1)/(4) \\ (1)/(4)=(1)/(4)\text{ (true)} \end{gathered}`

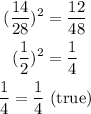
Since the relation is true, so the rectangles are similar.