Question

6) How long will it take for an investment to double in value if it earns 4.75% compoundedcontinuously?A) 14.593 yearsB) 15.711 years C) 23.129 years D) 7.296 years

Answer 1

A quantity that is compounded continuously follows the next equation:

`A=Pe^(rt)`

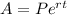
Where:

`\begin{gathered} A=\text{ amount in time ''t''} \\ P=\text{ initial amount} \\ r=\text{ rate of interest in decimal form} \\ t=\text{ time} \end{gathered}`

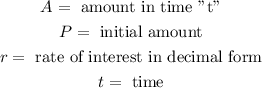
Now, the interest rate in decimal notation is determined by dividing the percentage by 100:

`r=(4.75)/(100)=0.0475`

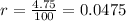
Now, we are asked to determine the time required for the quantity to double. Therefore, we need to determine "t" when:

`A=2P`

Substituting in the formula we get:

`2P=Pe^(rt)`

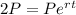
Now, we can cancel out the "P":

`2=e^(rt)`

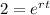
Now, we solve for "t". First, we take the natural logarithm to both sides:

`ln2=lne^(rt)`

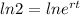
Now, we use the following property of logarithms:

`lnx{}^y=ylnx`

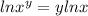
Applying the property we get:

`ln2=rtlne`

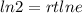
We have that:

`lne=1`

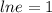
Therefore:

`ln2=rt`

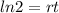
Now, we divide both sides by "r":

`(ln2)/(r)=t`

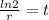
Now, we substitute the value of "r":

`(ln2)/(0.0475)=t`

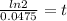
Solving the operations:

`14.593=t`

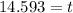
Therefore, the right option is A.