ANSWER :
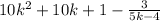
EXPLANATION :
From the problem, we have an expression :
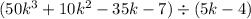
The divisor is (5k - 4)
Step 1 :
Divide the 1st term by the first term of the divisor.
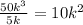
The result is 10k^2
Step 2 :
Multiply the result to the divisor :
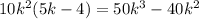
Step 3 :
Subtract the result from the polynomial :
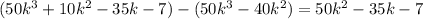
Now we have the polynomial :

Repeat Step 1 :

The result is 10k
Repeat Step 2 :
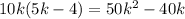
Repeat Step 3 :
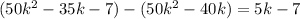
Now we have the polynomial :
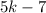
Repeat Step 1 :

The result is 1
Repeat Step 2 :
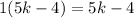
Repeat Step 3 :

Since -3 is a number, this will be the remainder.
Collect the bold results we had from above :
(10k^2 + 10k + 1) remainder -3
Note that the remainder can be expressed as remainder over divisor.
That will be :
