The Solution:
The Regression Model that best fits the data given in the question is
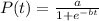
From the Desmos plotter analysis attached above, we have that

So, by substituting the values of the parameters, we get the required logistic Regression Model is given below:
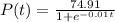
b. The model predicts that the population of California in 2025 will be:
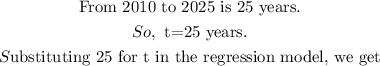
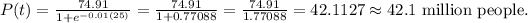
So, the population of California in 2025 will be 42.1 million people.
c. To find when the model predicts that the population of California will be 40 million,
we shall substitute 40 (in millions) for P in the model, and find t as below:
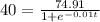
Cross multiplying, we get
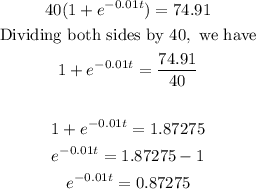
Taking the ln of both sides, we get
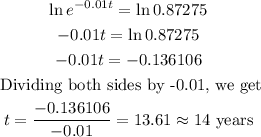
So, 14 years from 2010 will be in the year 2024
d. According to the model, the carrying capacity for California's capacity is 74.9 million people.