Question

-What is the product of (a - 1) and (2a + 2)?A 2(a2 - 2)B 2(a2 - 1)C a2 + 4a - 2D2a2 - 4a - 2-

Answer 1

The product of the sum and difference binomials is

`(x-y)(x+y)=x^2-y^2`

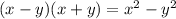
We will use this rule to solve the question

We need to find the product of (a - 1) and (2a + 2)

At first, we will take 2 as a common factor from the second bracket

`\begin{gathered} 2a+2=2((2a)/(2)+(2)/(2)) \\ 2a+2=2(a+1) \end{gathered}`

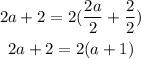
Now, we will multiply (a - 1) by 2(a + 1)

`(a-1)(2a-2)=2(a-1)(a+1)`

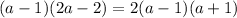
By using the rule of the product of the sum and difference above, then

`\begin{gathered} 2(a-1)(a+1)=2(a^2-1^2) \\ 2(a-1)(a+1)=2(a^2-1) \end{gathered}`

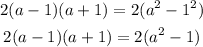
The answer is B