Question

A full tea cup has a mass of 0.40 kg. If the full cup applies a pressure of 1000.the radius of the circular ring imnrinted on the table?

Answer 1

Given:

The mass of the cup, m=0.40 kg

The pressure applied by the cup, P=1000 N/m²= 1000 Pa

To find:

The radius of the ring imprinted on the table.

Step-by-step explanation:

The pressure is defined as the force per unit area.

Thus the pressure applied by the cup is given by,

`\begin{gathered} P=(F)/(A) \\ =(mg)/(\pi r^2) \end{gathered}`

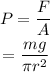
Where A is the area of the ring, g is the acceleration due to gravity, and r is the radius of the ring.

On rearranging the above equation,

`r=\sqrt{(mg)/(P\pi)}`

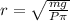
On substituting the known values,

`\begin{gathered} r=\sqrt{(0.40*10)/(1000\pi)} \\ =0.036\text{ m} \\ =3.6\text{ cm} \end{gathered}`

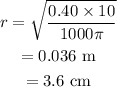
Final answer:

Thus the radius of the ring imprinted on the table is 3.6 cm

Therefore the correct answer is option 3.