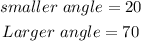SOLUTION
Given the question in the image, the following are the solution steps to answer the question.
STEP 1: Define complementary angles
When the sum of two angles is 90°, then the angles are known as complementary angles.
STEP 2: Write the pairs of the angles formed
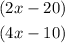
STEP 3: find the value of x
Following the definition in step 1, this goes that;
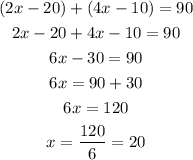
STEP 4: Find the two pair of angles
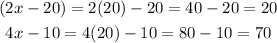
Therefore,