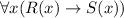Question

Using the predicate symbols shown and appropriate quantifiers, write each English language statement asa predicate wff. (The domain is the whole world.)B(x): x is a ballR(x): x is roundS(x): x is a soccer ballc. All soccer balls are round.d. Some balls are not round.e. Some balls are round but soccer balls are not.f. Every round ball is a soccer ball.

Answer 1

c) The statement "All soccer balls are round" is equivalent to "For all x, if S(x) then R(x)" and it can be written in predicate wff as

`\forall x\text{ (S(x)}\rightarrow R(x))`

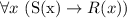
d) The statement "Some balls are not round" is equivalent to "There exist some x such that B(x) and not R(x)", which can be written in predicate wff as

`\mathfrak{\Im }x(B(x)\wedge\urcorner R(x))`

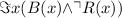
e) The statement "Some balls are round but soccer balls are not" is equivalent to "There exist x such that B(x) and R(x) and there exist x such that S(x) and not R(x)", can be written in prediacte wff as

`\mathfrak{\Im }x(B(x)\wedge R(x))\wedge\mathfrak{\Im }x(S(x)\wedge\urcorner R(x))`

f) The statement "Every round ball is a soccer ball" is equivalent to "For all x, if R(x) then S(x)", can be written in prediacte wff as

`\forall x(R(x)\rightarrow S(x))`