Step-by-step explanation
The television has a diagonal that measures 36 inches:
And the ratio is 4:3
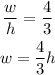
We can use the Pythagorean theorem to find the height of the TV:
![\begin{gathered} 36^2=h^2+w^2 \\ 36^2=h^2+((4)/(3)h)^2 \\ 36^2=h^2(1+(4^2)/(3^(2))) \\ 1296=h^2(1+(16)/(9)) \\ 1296=h^2*(25)/(9) \\ h^2=1296*(9)/(25) \\ h=\sqrt[]{1296*(9)/(25)}=21.6 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/ji3ro0afpvtaefq3zghhqic52u72agyg6y.png)
The height of the TV is 60 inches. It's width is:
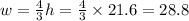
w=80 inches
Therefore the area of the TV is
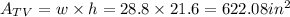
The move has an aspec ratio of 25:1 shown as a pillarboxed image. This means that this is what we see:
So we know that the image height is the same as the TV's, 21.6 inches.
The relation between it's height and it's width is:
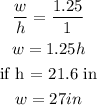
The area of the image is:
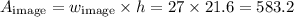
The area of the two blackbars is the difference between the area of the TV and the area of the image:

Since we need to find the area of just one blackbar, we just have to divide the area of both blackbars by 2:
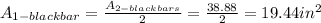
Answer
• Area of the TV: ,622.08 in²
,
• Area of the image: ,583.2 in²
,
• Area of one blackbar: ,19.44 in²