Question

Match the blanks to their missing phrases to complete the proof

Answer 1

blank A: a^2 + b^2 = c^2

blank B: Definition of unit circle

blank C: sin θ = y/1 = y

Step-by-step explanation:

In order to prove the identity given, we first start with Pythagoras's theorem

`a^2+b^2=c^2`

which is blank a.

Next, we apply the theorem to the circle to get

`x^2+y^2=r^2`

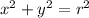
then we make the substitutions.

Since it is a unit circle r = 1 (blank B) and using trigonometry gives

`\cos \theta=(x)/(r)=(x)/(1)=x`
`\boxed{x=\cos \theta}`

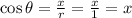
and

`\sin \theta=(y)/(r)=(y)/(1)=y`

`\boxed{y=\sin \theta}`

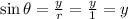
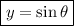
which is blank C.

With the value of x, y and r in hand, we now have

`x^2+y^2=1`
`\rightarrow\sin ^2\theta+\cos ^2\theta=1`

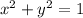
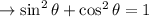
Hence, the identity is proved.