Question

The famous mathematician Gauss is credited with deriving a formula for determining the the sum of the first n counting numbers. If the sum of the first 100 counting numbers is 5050, what is the difference between the sum of all of the even counting numbers and the odd counting numbers less than 101? Start by making the problem simpler and look for patterns. Describe how you came to your solution.

Answer 1

Given:

The sum of the first 100 counting numbers is 5050.

To find:

The difference between the sum of all of the even counting numbers and the odd counting numbers less than 101.

Step-by-step explanation:

Let us find the sum of all of the even counting numbers from 1 to 101.

The series is,

`S_1=2+4+6+....+100`

It can be written as,

`S_1=2(1+2+3+.....+50)`

Using the formula,

`\begin{gathered} 1+2+3+.....+n=(n(n+1))/(2) \\ S_1=2(1+2+3+....+50)=2[(50(50+1))/(2)] \\ S_1=50(51) \\ S_1=2550........(1) \end{gathered}`

Next, let us find the sum of all of the odd counting numbers.

`\begin{gathered} S_2=Total-Sum\text{ of all even numebrs} \\ S_2=5050-2550 \\ S_2=2500.......(2) \end{gathered}`

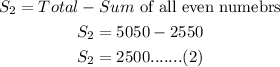
So, the difference between the sum of all of the even counting numbers and the odd counting numbers less than 101 is

`\begin{gathered} S_1-S_2=2550-2500 \\ =50 \end{gathered}`

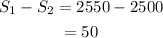
Final answer:

The difference between the sum of all of the even counting numbers and the odd counting numbers less than 101 is 50.