The slope of the tangent line at the point x = a of the function f(x) is f'(a).
We are given the function:

Computing the first derivative:
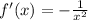
The slope of the tangent line at (1, 1), that is, where x = 1 is:

The tangent line and the normal line are perpendicular to each other. If their respective slopes are m1 and m2, then:

We have calculated m1 = -1, calculate m2:

Now we know the slope of the normal line. We need to find its equation. Use the point-slope formula:
y - k = m(x - h)
Where m is the known slope and (h, k) is a point of the line. We are given the point (1, 1), thus:
y - 1 = 1(x - 1) = x - 1
Adding 1:
y = x
Answer: D. x