Question

To save money for her son's college tuition, Mary invests $98 every month in an annuity that pays 6.1% interest, compounded monthly. Payments will be made at the end of each month. Find the total value of the annuity in 21 years.

Answer 1

Given

Monthly deposit = $98

Rate = 6.1%

Number of years = 21

Find

Total value of the annuity in 21 years.

Step-by-step explanation

Total value of annuity is given by

`FV=A[((1+(r)/(m))^(mt)-1)/((r)/(m))]`

where FV is a future value

so ,

`\begin{gathered} FV=98[((1+(0.061)/(12))^(12*21)-1)/((0.061)/(12))] \\ \\ \end{gathered}`

now solve this to obtain the future value .

`\begin{gathered} FV=98*509.227229162 \\ FV=49904.26 \end{gathered}`

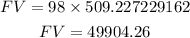
Final Answer

Therefore , the future value is $49904.27