Question

Help me out with this question..this is a k11..remember this is a practice question not a graded one

Answer 1

Each flight has a probability of 60% or 0.6 of being on time. This means that its complement, or the probability that the flight isn't on time is:

`\text{\textasciitilde{}P(on time)}=1-0.6=0.4`

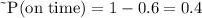
It is 40% or 0.4. "~P(on time)" stands for the probability of the flight not being on time.

1. The probability that at least 2 flights are on time is:

To find the probability that 2 or more flights are on time we can fight the probability that "0" or "1" are not on time.

`P(0\text{ on time)}=0.4^9=0.000262144`
`\begin{gathered} P(1\text{ on time})=(9!)/(1!\cdot(9-1)!)\cdot0.6\cdot(0.4)^8 \\ P(1\text{ on time)}=9\cdot0.6\cdot(0.4)^8=0.003538944 \end{gathered}`
`\begin{gathered} P(1\text{ or less on time)}=P(0\text{ on time)}+P(1\text{ on time)} \\ P(1\text{ or less on time)}=0.000262144+0.003538944=0.003801088 \end{gathered}`

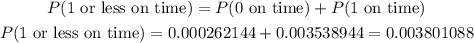
The probability of 2 or more flights are on time is:

`P(2\text{ or more on time)}\cdot=1-0.003801088=0.996198912`

The probability of 2 flights or more are on time is 0.996198912

2.

We need to calculate the probabilities of 7,8 and 9 flights are on time and then subtract by 1.

`\begin{gathered} P(7)=(9!)/(7!\cdot(9-7)!)\cdot0.6^7\cdot0.4^2 \\ P(7)=36\cdot0.6^7\cdot0.4^2=0.161243136 \end{gathered}`
`\begin{gathered} P(8)=(9!)/(8!\cdot(9-8)!)\cdot0.6^8\cdot0.4 \\ P(8)=9\cdot0.6^8\cdot0.4=0.060466176 \end{gathered}`
`P(9)=0.6^9=0.010077696`

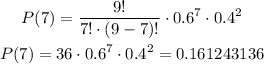
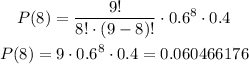
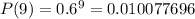
The probability of at most 6 flights are on time is:

`\begin{gathered} P(6\text{ or less on time) = 1 - (}P(7)+P(8)+P(9)) \\ P(6\text{ or less on time) = 1-(0.161243136+0.060466176+0.010077696)=}0.768212992 \end{gathered}`

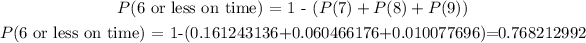
The probability of 6 or less are on time is 0.768212992.

3.

The probability of exactly 5 flights are on time is:

`\begin{gathered} P(5)=(9!)/(5!(9-5)!)0.6^5\cdot0.4^4 \\ P(5)=126\cdot0.6^5\cdot0.4^4=0.250822656 \end{gathered}`

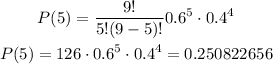
The probability of exactly 5 flights are on time is 0.250822656.