Given parameters:

We can now apply the formula below to calculate the payment amount per period
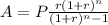
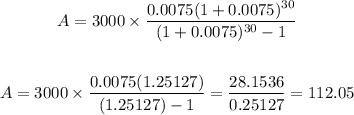
Thus his monthly payment will be $112.05
But since we have to get the interest on the first month's pay,
The interest is
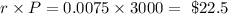
Thus, $22.50 is the interest on the first month's payment