Question

Two trees are leaning on each other in the forest. One tree is 19 feet long and makes a 32° angle with the ground. The second tree is 16 feet long.What is the approximate angle, x, that the second tree makes with the ground?

Answer 1

39º

1) Considering what's been given we can sketch this out:

From these trees leaning on each other, we can visualize a triangle (in black).

2) So now, since we need to find the other angle, then we need to apply the Law of Sines to find out the missing angle:

`\begin{gathered} (a)/(\sin(A))=(b)/(\sin (B)) \\ (16)/(\sin(32))=(19)/(\sin (X)) \\ 16\cdot\sin (x)=19\cdot\sin (32) \\ (16\sin(X))/(16)=(19\sin (32))/(16) \\ \sin (X)=(19\sin(32))/(16) \\ \end{gathered}`

As we need the measure of the angle, (not any leg) then we need to use the arcsine of that quotient:

`\begin{gathered} X=\sin ^(-1)((19\cdot\sin (32))/(16)) \\ X=38.996\approx39 \end{gathered}`

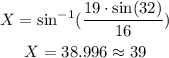
3) Hence, the approximate measure of that angle X is 39º