Question

In the figure to the right, what value of x makes G the incenter of triangle JKL. See image below

Answer 1

We were given the following information:

LT = 12

GL = 13

GR = x - 3

The incenter of a triangle refers to the intersection point of all interior angle bisectors of the triangle. The incenter is equidistant to the sides, they are all the same

If triangle JKL has G as its incenter, the following will be found to be true:

`|GR|\cong|GS|\cong|GT|`

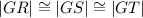
However, we were not given any of the above distances GR, GS & GT. We can obtain GT by using the Pythagoras Theorem on the triangle GTL as shown below:

`\begin{gathered} |GT|^2=|GL|^2-|LT|^2 \\ |GT|^2=13^2-12^2 \\ |GT|^2=169-144 \\ |GT|^2=25 \\ \text{Take the square root of both sides, we have:} \\ |GT|=\sqrt[]{25} \\ |GT|=5 \\ \\ \therefore|GT|=5 \end{gathered}`

Since GT equals 5, it implies that GS & GT will also equal 5

We will obtain the value of ''x'' as shown below: