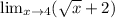Answer:
The correct answer is the third option:
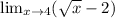
Step-by-step explanation:
We have the function:
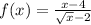
In the numerator, we have x - 4. We can rewrite it as a difference of squares, since:
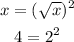
Thus:
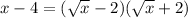
Then, the limit:
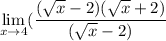
We can cancel out the terms, since we are taking limit, this is, numbers that infinitely close to 4, bt never 4. This way we can cancel the terms, and get: