Question

Please help me with this question:Graph the function F(x) = x^2 + 4x - 12 on the coordinate plane by finding the important points below.Be sure to show all steps in your calculations.(a)What are the x-intercepts?(b)What is the y-intercept?(c)What is the maximum or minimum value?(d)Use the points to graph the function.

Answer 1

Given the function:

`f(x)=x^2+4x-12`

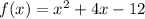
Let's graph the function.

Let's find the following:

• (a). x-intercepts:

The x-intercepts are the points the function crosses the x-axis.

To find the x-intercepts substitute 0 for f(x) and solve for x.

`\begin{gathered} 0=x^2+4x-12 \\ \\ x^2+4x-12=0 \end{gathered}`

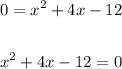
Factor the left side using AC method.

Find a pair of numbers whose sum is 4 and product is -12.

We have:

6 and -2

Hence, we have

`\begin{gathered} (x+6)(x-2)=0 \\ \\ \end{gathered}`

Equate the individual factors to zero and solve for x.

`\begin{gathered} x+6=0 \\ Subtract\text{ 6 frm both sides:} \\ x+6-6=0-6 \\ x=-6 \\ \\ \\ x-2=0 \\ Add\text{ 2 to both sides:} \\ x-2+2=0+2 \\ x=2 \end{gathered}`

Therefore, the x-intercepts are:

x = -6 and 2

In point form, the x-intercepts are:

(x, y) ==> (-6, 0) and (2, 0)

• (b). The y-intercept.

The y-intercept is the point the function crosses the y-axis.

Substitute 0 for x and solve f(0) to find the y-intercept:

`\begin{gathered} f(0)=0^2+4(0)-12 \\ \\ f(0)=-12 \end{gathered}`

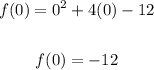
Therefore, the y-intercept is:

y = -12

In point form, the y-intercept is:

(x, y) ==> (0, -12)

• (c). What is the maximum or minimum value?

Since the leading coefficient is positive the graph will have a minimum value.

To find the point where it is minimum, apply the formula:

`x=-(b)/(2a)`

Where:

b = 4

a = 1

Thus, we have:

`\begin{gathered} x=-(4)/(2(1)) \\ \\ x=-(4)/(2) \\ \\ x=-2 \end{gathered}`

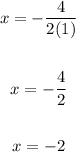
To find the minimum values, substitute -2 for x and solve for f(-2):

`\begin{gathered} f(-2)=(-2)^2+4(-2)-12 \\ \\ f(-2)=4-8-12 \\ \\ f(-2)=-16 \end{gathered}`

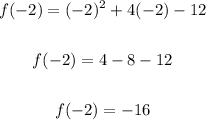
Therefore, the minimum value is at:

y = -16

Using the point form, we have the minimum point:

(x, y) ==> (-2, -16).

• (d). Use the points to plot the graph.

We have the points:

(x, y) ==> (-6, 0), (2, 0), (0, -12), (-2, -16)

Plotting the graph using the points, we have: