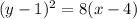Question

a) which is equation of the parabola? b) name the focus and directrix ? c) name vertex and axis of symmetry?

Answer 1

The equation of the parabola whose axis of symmetry is parallel to x-axis is

`(y-k)^2=4p(x-h)`

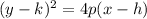
where the focus is

`\text{focus}=(h+p,k)`

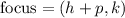
and the directrix is

`x=h-p`

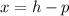
In our case, the focus is (6,1) and the directrix is x =2; therefore, we have

`(6,1)=(h+p,k)`

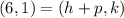
and

`h-p=2`

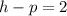
These equations give

`k=1,h=4,p=2`

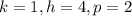
Hence, the equation of the parabola is

`(y-1)^2=8(x-4)`