Using the formula
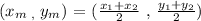
x₁= 10 y₁=12 Xm=2 Ym = 8
x₂ = ? y₂=?
Substituting and solving for x₂
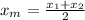
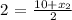
Multiply both-side of the equation by 2
4 = 10 + x₂
subtract 10 from both-side of the equation
-6 = x₂
x₂= -6
Similarly, substituting and solving for y₂
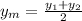
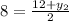
Multiply both-side of the equation by 2
16 = 12 + y₂
Subtract 12 from both-side of the equation
4 = y₂
y₂= 2
Hence; coordinates of B are;
B(x,y) = ( -6, 2)