Albert
Compound interest formula:

where:
A: final amount
P: principal
r: annual interest rate, as a decimal
t: time in years
n: number of times interest applied per year
Substituting with P = $1000, r = 0.012 (= 1.2/100), n = 12 (interest is compounded monthly), t = 10 years, we get:
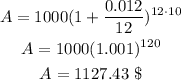
If $500 lost 2%, then it keeps 98% of its original value, that is,
$500x98% = $490
Continuous compound formula:
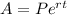
where the variables have the same meaning as before.
Substituting with P = $500, r = 0.008 ( = 0.8/100), and t = 10 years, we get:
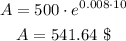
The balance of Albert’s $2000 after 10 years is:
$1127.43 + $490 + $541.64 = $2159.07
Marie
Substituting in the compound interest formula with P = $1500, r = 0.014 (= 1.4/100), n = 4 (interest is compounded quartely), t = 10 years, we get: