Question

A massless scaffold is held up by a wire at each end. The scaffold is 12 m long. A300-N box sits 4.0 m from the left end. What is the tension in each wire?1) left wire = 100 N; right wire = 200 N2) left wire = 200 N; right wire = 100 N3) left wire = 900 N; right wire = 2700 N4) left wire = 2700 N; right wire = 900 N

Answer 1

Free body diagram:

Given data:

Length of massless scaffold (end to end) L=12 m.

Weight of box m=300 N.

Length of massless scaffold (center to end) l=6 m.

As, the box sits 4.0 m from the left end, the distance of the box from the center of massless scaffold is given as,

`\begin{gathered} r=6.0\text{ m}-4.0\text{ m} \\ =2.0\text{ m} \end{gathered}`

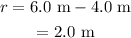
Balancing force in y direction,

`T_1+T_2=300\text{ N}\ldots(1)`

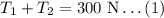
The torque is given as,

`\tau=perpendicular\text{ distance}* force`

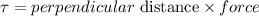
Therefore, torque along the center of massless scaffold is given as,

`\begin{gathered} \Sigma\tau=0 \\ l* T_1+r*(300\text{ N})-l*\tau_2=0 \\ 6* T_1+2*(300\text{ N})-6* T_2=0 \\ 6T_1+600\text{ N}-6T_2=0 \\ 6(T_1+100\text{ N}-T_2)=0 \\ T_1+100\text{ N}-T_2=0 \\ T_1-T_2=-100\text{ N}\ldots(2) \end{gathered}`

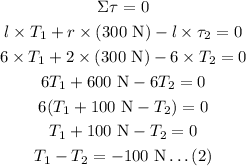
Adding equation (1) and (2),

`\begin{gathered} (T_1+T_2)+(T_1-T_2)=300\text{ N}-100\text{ N} \\ T_1+T_1+T_2-T_2=200\text{ N} \\ 2T_1=200\text{ N} \\ T_1=\frac{200\text{ N}}{2} \\ T_1=100\text{ N} \end{gathered}`

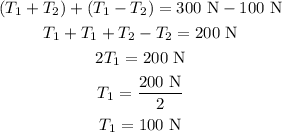
Substituting T1 in equation (1) we get,

`\begin{gathered} 100\text{ N}+T_2=300\text{ N} \\ T_2=300\text{ N}-100\text{ N} \\ T_2=200\text{ N} \end{gathered}`

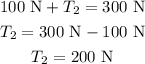
Therefore, tension in left wire is 100 N and tension on right wire is 200 N. Hence, option (1) is the correct choice.