Question

Use the factor theorem to find all real zeros for the given polynomial and one of it's factors.Polynomial: f(x)=3x^3+x^2-20x+12 Factor: x+3List the zero's from smallest to largest. If a zero is not an integer write it as a fraction.The zeros are Answer , Answer and Answer

Answer 1

the zeros are -3, 2/3, and 2

Step-by-step explanation:
`\begin{gathered} f(x)=3x^3+x^2\text{ - 20x + 12} \\ We\text{ n}eed\text{ to test if x + 3 is a factor} \end{gathered}`

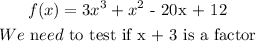
x + 3 = 0

x = -3

We will susbtitute -3 for x in the polynomial:

`\begin{gathered} f(-3)=3(-3)^3+(-3)^2\text{ - 20(-3) + 12} \\ f(-3)=\text{ 3(-27) + 9 + 60 + 12 } \\ f(-3)\text{ = 0} \end{gathered}`

Since the remainder is zero, this means x + 3 is a factor of the polynomial

Using synthetic division to get the remaining factor after factoring (x + 3):

`3x^3+x^2-20x+12=(3x^2\text{ - 8x + 4)(x + 3)}`

Using the factor theorem to find other factors:

`\begin{gathered} f(x)=3x^2\text{- 8x + 4} \\ \text{factors of 4 = }\pm1,\text{ }\pm2,\text{ }\pm4 \\ \text{Let's try x = }1 \\ f(1)\text{ = }3(1)^2\text{- 8(1) + 4 = 3(1) - 8 + 4 = -1} \\ f(2)\text{ = }3(2)^2\text{- 8(2) + 4 = 3(4) - 16 + 4 = 0} \\ \text{Since f(2) = 0} \\ x\text{ = 2} \\ x\text{ - 2 = 0 . As a result, (x - 2) is a factor of the polynomial} \end{gathered}`

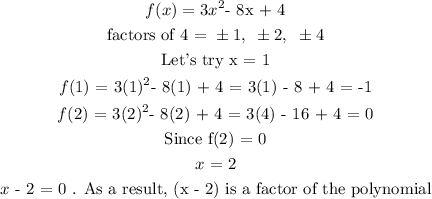
Using synthetic division:

`3x^2\text{- 8x + 4 = (x - 2)(3x -2)}`
`\begin{gathered} 3x^3+x^2-20x+12=(3x^2\text{ - 8x + 4)(x + 3)} \\ 3x^3+x^2-20x+12=(x-2)(3x-2\text{)(x + 3)} \end{gathered}`
`\begin{gathered} \text{x - 2 = 0; x = 2} \\ 3x\text{ - 2; x = 2/3} \\ x\text{ + 3; x = -3} \\ \text{The zeros are 2, 2/3 and -3} \\ \end{gathered}`

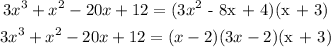
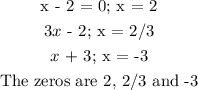
From the smallest to the largest, the zeros are -3, 2/3, and 2