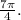The cosine function is:
![\[ f(x) = 3 \cos\left((8)/(7)x\right) + 2 \]](https://img.qammunity.org/2023/formulas/mathematics/college/66h85r037c5aornhy3jsdzpmy2h3sm50sa.png)
To write a cosine function with a midline of 2, an amplitude of 3, and a period of
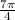 , you can use the general form of a cosine function:
, you can use the general form of a cosine function:
![\[ f(x) = A \cos\left((2\pi)/(B)(x - C)\right) + D \]](https://img.qammunity.org/2023/formulas/mathematics/college/ox1f0mk76ycuhf2234qi9s3qve2bhpqngi.png)
In this case:
- The midline is 2, which means D = 2 .
- The amplitude is 3, which means |A| = 3 . We'll choose A = 3 since cosine is an even function.
- The period is
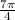 , which means
, which means
 Solving for B :
Solving for B :
![\[ B = (2\pi)/((7\pi)/(4)) = (8)/(7) \]](https://img.qammunity.org/2023/formulas/mathematics/college/1lh2liciwfl3rjly3ftpomjayf2gehzomg.png)
So,
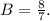
- We don't need to shift the graph left or right, so C = 0 .
Now, we can write the cosine function:
![\[ f(x) = 3 \cos\left((8)/(7)x\right) + 2 \]](https://img.qammunity.org/2023/formulas/mathematics/college/66h85r037c5aornhy3jsdzpmy2h3sm50sa.png)
This function has a midline of 2, an amplitude of 3, and a period of