We can break apart the figure into 4 separate figures and find the area of each of these individual figures. Then sum to get area of total figure.
We break apart the figure as shown below:
First,
Area of Triangle = 0.5 * base * height
Area of Rectangle = base * height
Now, let's find each of the Areas A through D:
Area of A:
To find the base of this triangle, we have to use pythagorean theorem. By which we can write:
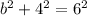
Where b is the base. let's solve for b:
![\begin{gathered} b^2+16=36 \\ b^2=36-16 \\ b^2=20 \\ b=\sqrt[]{20} \\ b=\sqrt[]{4}\sqrt[]{5} \\ b=2\sqrt[]{5} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/1mcmz55lo4or5csdjge7to8jp8bispz1qz.png)
Area is
![\begin{gathered} 0.5\cdot\text{base}\cdot\text{height} \\ =(1)/(2)\cdot2\sqrt[]{5}\cdot4 \\ =4\sqrt[]{5} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/pmnpwnwwplj5xvd7n40loh2nzieh30aabd.png)
Area of B:
This is a rectangle with base = 10 and height 4, so the area is:
Area = 4 * 10 = 40
Area of C:
Area of C is exactly same as area of B, base is 10 and height is 4. So,
Area = 4 * 10 = 40
Area of D:
Like area of A, we have to find the base of the triangle first, using pythagorean theorem. We can write:
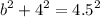
Solving for b:
![\begin{gathered} b^2+4^2=4.5^2 \\ b^2+16=20.25 \\ b^2=(17)/(4) \\ b=\frac{\sqrt[]{17}}{\sqrt[]{4}} \\ b=\frac{\sqrt[]{17}}{2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/83kdeqse61he3gchu6ohe5xyz8ye4a8qy9.png)
Now, area of triangle is:
![A=(1)/(2)(\frac{\sqrt[]{17}}{2})(4)=\sqrt[]{17}](https://img.qammunity.org/2023/formulas/mathematics/college/qi77y0tiu45y2icj6njie3j748xnicdjyu.png)
Area of whole figure:
![\begin{gathered} 4\sqrt[]{5}+40+40+\sqrt[]{17} \\ =80+4\sqrt[]{5}+\sqrt[]{17} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/y6uqxdx5v59xr56pazv7kh8xf66v9dwie4.png)
Since mulch costs $3 per square feet, we have to multiply the area by "3", so we have:
![3*(80+4\sqrt[]{5}+\sqrt[]{17})\approx279.202](https://img.qammunity.org/2023/formulas/mathematics/college/es9pe023gs8omzxbubvfy0p115fhafwk0w.png)
It will cost around:
$279.20