Question

Solve the system.x + y + 2z = -1x+ y + 8z = -7(x-9y - 2z = -37

Answer 1

Given the three variable simultaneous equations;

`\begin{gathered} x+y+2z=-1\ldots\ldots.i \\ x+y+8z=-7\ldots\ldots.ii \\ x-9y-2z=-37\ldots\ldots.iii \end{gathered}`

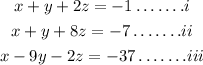
To solve;

let's solve for z by subtracting equation i from ii;

`\begin{gathered} x+y+8z-(x+y+2z)=-7-(-1) \\ x-x+y-y+8z-2z=-7+1 \\ 6z=-6 \\ (6z)/(6)=(-6)/(6) \\ z=-1 \end{gathered}`

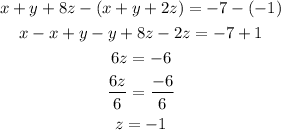
next let's solve for y by subtracting equation i from iii;

`\begin{gathered} x-9y-2z-(x+y+2z)=-37-(-1) \\ x-x-9y-y-2z-2z=-37+1 \\ -10y-4z=-36 \\ \text{ since z=-1} \\ -10y-4(-1)=-36 \\ -10y+4=-36 \\ -10y+4-4=-36-4 \\ -10y=-40 \\ (-10y)/(-10)=(-40)/(-10) \\ y=4 \end{gathered}`

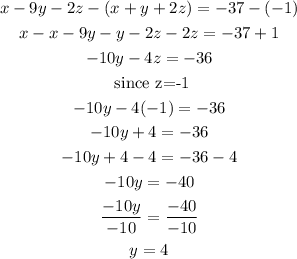
We have z and y, to get x let us substitute te values of y and z into equation i;

`\begin{gathered} x+y+2z=-1 \\ x+(4)+2(-1)=-1 \\ x+4-2=-1 \\ x+2=-1 \\ x+2-2=-1-2 \\ x=-3 \end{gathered}`

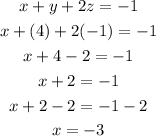
Therefore the values of x, y and z are;

`\begin{gathered} x=-3 \\ y=4 \\ z=-1 \end{gathered}`

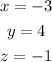
Answer is A.