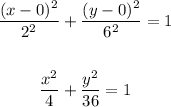Question

Find an equation of an ellipse satisfying the given conditions Vertices: (0 - 6) and (0.6) Length of minor axis: 8

Answer 1

As the given vertices are at a distance of 12 units:

As the major axis is vertical you have the next generall equation:

`((x-h)^2)/(b^2)+((y-k)^2)/(a^2)=1`

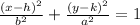
To find the center (h,k) of the ellipse use the coordinates of that vertices as follow:

`((0+0)/(2),(6-6)/(2))=(0,0)`

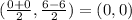
Now use the distance between those vertices to find a:

`a=(12)/(2)=6`

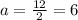
b is the distance of minor axis divided into 2:

`b=(4)/(2)=2`

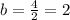
Then, you get the next equation for the given ellipse:

`\begin{gathered} ((x-0)^2)/(2^2)+((y-0)^2)/(6^2)=1 \\ \\ (x^2)/(4)+(y^2)/(36)=1 \end{gathered}`