Question

Describe two methods you could use to solve for `x` in `1.12^{x}=20`

Answer 1

Step-by-step explanation:

Given;

We are given the following equation;

`1.12^x=20`

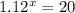
Required;

We are required to describe two methods which can be used to solve for x in this equation.

Step-by-step solution;

We can solve for the variable x by taking the natural log of both sides of the equation. This is shown below;

`1.12^x=20`

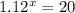
We take the natural log of both sides;

`ln1.12^x=ln20`

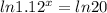
Next we apply the log rule;

`\begin{gathered} If: \\ log_bx^a \\ Then: \\ alog_bx \end{gathered}`

Therefore, our equation is now refined and becomes;

`xln1.12=ln20`

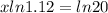
Divide both sides by ln(1.12);

`x=(ln(20))/(ln(1.12))`

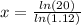
A second method is to express it as a logarithmic equation;

`1.12^x=20`

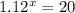
We shall apply the log rule which is;

`\begin{gathered} If: \\ log_bx=a \end{gathered}`
`\begin{gathered} Then: \\ b^a=x \end{gathered}`

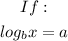
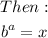
For example;

`\begin{gathered} If: \\ log_(10)100=2 \end{gathered}`
`\begin{gathered} Then: \\ 10^2=100 \end{gathered}`

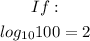
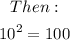
Therefore, for the equation given;

`\begin{gathered} If: \\ 1.12^x=20 \end{gathered}`
`\begin{gathered} Then: \\ log_(1.12)20=x \end{gathered}`

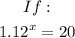
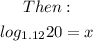
Note that both solutions can be simplified eventually with the use of a calculator.

ANSWER:

(1) By taking the natural log of both sides

(2) By expressing the equation as a logarithmic equation