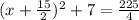ANSWER
225/4
Step-by-step explanation
To complete the square we want to write a part of the equation in the form:
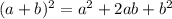
The second term squared is the one we have to add to the equation in order to complete the square.
In this case, the coefficient of x is 15, so b is:
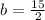
And b²:
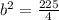
If we add 225/4 to both sides of the equation:
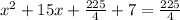
We complete the square: