Question

ans (alpha particles) at Figure 127 Exercises 12.6. complete the following: Find the intercepts and domain and perform the symmetry test (a) 9x^2 - 16y^2 = 144

Answer 1

We have that the general equation of the hyperbola is the following:

`(x^2)/(a^2)-(y^2)/(b^2)=1`

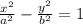
where 'a' and '-a' are the x-intercepts.

In this case, we have the following equation:

`9x^2-16y^2=144`

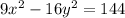
then, we have to divide both sides by 144 to get on the right side 1, thus, we have the following:

`\begin{gathered} (9x^2-16y^2=144)((1)/(144)) \\ \Rightarrow(9)/(144)x^2-(16)/(144)y^2=1 \\ \Rightarrow(x^2)/(16)-(y^2)/(9)=1 \end{gathered}`

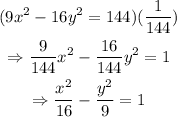
now, notice that we have that:

`a^2=16`

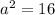
then, the x-intercepts are:

`\begin{gathered} a^2=16 \\ \Rightarrow a=\pm\sqrt[]{16}=\pm4 \\ a_1=4 \\ \text{and} \\ a_2=-4 \end{gathered}`

therefore, the x-intercepts are 4 and -4.

Now that we know that the intercepts are on those points, we can see that the hyperbola has the following graph:

we can see that the hyperbola is not defined between -4 and 4, therefore, the domain of the hyperbola is:

`(-\infty,-4\rbrack\cup\lbrack4,\infty)`

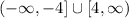
finally, to perform the symmetry test, we have to check first both axis simmetries by changing x to -x and y to -y:

`\begin{gathered} (x^2)/(16)-((-y)^2)/(9)=1 \\ \Rightarrow(x^2)/(16)-(y^2)/(9)=1 \\ then \\ ((-x)^2)/(16)-(y^2)/(9)=1 \\ \Rightarrow(x^2)/(16)-(y^2)/(9)=1 \end{gathered}`

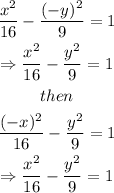
since the hyperbola got symmetry about the x-axis and the y-axis, we have that the hyperbola got symmetry about the origin