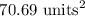Given:
m∠DEF = 36
DE = 15 units
Let's find the area of the sector.
To find the area of the sector, apply the formula:
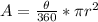
Where:
radius, r = DE = 15 units
θ = 36
Substitute values into the formula:
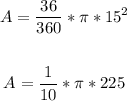
Solving further:
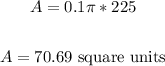
Therefore, the area of the sector rounded to the nearest hundredth is 70.69 square units
ANSWER: