ANSWER
Yes, it does.
Step-by-step explanation
We want to check if the data set displays an exponential behavior.
An exponential function is one in which the values of the range (y values) increase by a certain factor.
The general form of an exponential function is:
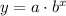
where a is the starting value
b = factor.
Now, we have to compare the data set with this kind of function.
To do that, we have to find a mock function of the data set using the first two data points to test each x value (domain) for each y value.
Basically, we will replace x in the function with a value and see if we get the correct y.
Therefore, when x = 0:
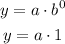
From the data set, we see that, when x = 0, y = 1:
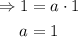
That is the value of a.
Now, let us try when x = 1:

From the data set, we see that, when x = 1, y = 3:
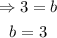
Now, we can say that we have an exponential function to test with:
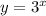
So, let us test for the remaining values of x and y and see if they match the function.
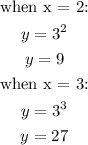
As we can see, each x value that goes into the function yields the exact y value as the data set. This means that the exponential function works for it.
Hence, the data set displays an exponential behavior.