we can do a triangle to solve the apothem
the upper angle is equal to 360 divided by 8 since 360 is a complete turn and an octagon is composed of 8 equal triangles, so is 45
now we take a triangle from the triangle to apply trigonometric ratios and solve a
the upper angle of the new triangle is the half of the original so is 45/2
now i will use the trigonometric ratio of tangent
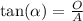
where alpha is the angle, O the opposite side drom the angle and a the adjacent side from the angle
so replacing
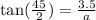
and solve for a
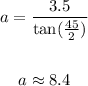
the aphotem is 8.4
and the formula of the area of the octagon is
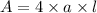
where a is the aphotem and l the measure f each side so 7
replacing

the area is 235.2 square units