hello
the standard equation of a straight line is given as y = mx + b
y = y-coordinate
x = x-coordinate
m = slope
b = intercept
the points given are (3, 3) and the slope = 2 / 3
y = mx + b
y = 3
x = 3
let's substitute in our values and solve for b
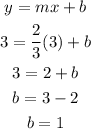
since we have the value of the slope, we can simply write the equation from y = mx + b to y = 2/3x + 1

this is the equation of the line.
but we can further simplify this by looking for the LCM of the denominators of the independent variables
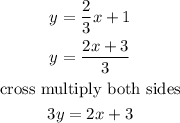
the equation can be rewritten as 3y = 2x + 3