The rate of change of a linear functions is given by:

where (x1,y1) and (x2,y2) are points through the graph.
Function 1.
From the table we have that the functions passes through the points (-11,8) and (-7,13), pluggin the values in the formula above we have:

Therefore the rate of change of functions 1 is 5/4
Function 2.
From the graph we notice that the functions passes through the points (-3,-4) and (1,-1), hence:
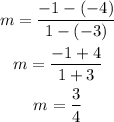
Therefore the rate of change of function 2 is 3/4.
Comparing both rates of change we conclude that Function 1 has the greater change of rate.