We have the points of a linear function and need to find the equation that represent.
Because it is a linear function, we can find its equation with two points.
We get the points (1,3) and (2,1):
![\begin{gathered} We\text{ call input as x and output as y:} \\ P_1=(x_1,y_1)=(1,3),P_2=(x_2,y_2)=(2,1) \\ y-y_1=((y_2-y_1))/((x_2-x_1))(x-x_1) \\ y-3=((1-3))/((2-1))(x-1) \\ y-3=-(2)/(1)(x-1)=-2(x-1) \\ y=-2x-2\cdot(-1)+3 \\ y=-2x+2+3 \\ y=-2x+5 \end{gathered}]()
We can check that the points (3,-1) and (4,-3) also satisfy the equation that we found above:
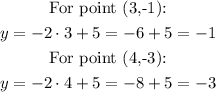
The above shows that the points satisfy the equation.
So, for input=n the output is:
![\text{output}=-2\cdot n+5]()