Question

2v²+8v=-7 i need 5 points to graph range solutions

Answer 1

Given the quadratic equation below

`\begin{gathered} 2v^2+8v=-7 \\ \Rightarrow2v^2+8v+7=0 \\ \therefore y=2v^2+8v+7 \end{gathered}`

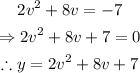
Note: y is function defined by v ( independent variable)

To plot the graph of the function above, we will take a range of values for v, i.e

`\begin{gathered} -2\le v\le2 \\ \text{The range}\Rightarrow-2,-1,0,1,2 \end{gathered}`

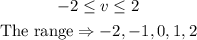
Given the range of values above, find the corresponding y-values . This can be done by substituting for v in the quadratic equation above

`\begin{gathered} \text{when v=-2} \\ y=2(-2)^2+8(-2)+7=2(4)-16+7=8+7-16=15-16=-1 \end{gathered}`
`\begin{gathered} \text{When v=-1} \\ y=2(-1)^2+8(-1)+7=2(1)-8+7=2+7-8=9-8=1 \end{gathered}`
`\begin{gathered} \text{When v=0} \\ y=2(0)^2+8(0)+7=0+0+7=7 \end{gathered}`
`\begin{gathered} \text{When v=1} \\ y=2(1)^2+8(1)+7=2+8+7=17 \end{gathered}`
`\begin{gathered} \text{When v=2} \\ y=2(2)^2+8(2)+7=2(4)+16+7=8+16+7=31 \end{gathered}`

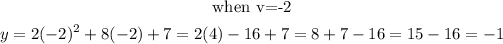
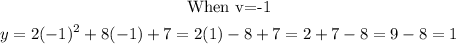
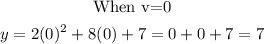
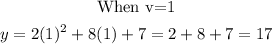
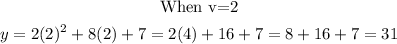
The table of values is shown below

Hence, the graph of the solution is shown below