Suppose that the sides of the rectangle have lengths x and y, and that the measure of the side parallel to the creek is y, as shown in the drawing below
The total length of the fence, according to the drawing, is:
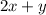
Since there is 120 feet of fencing available, then:
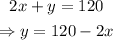
On the other hand, the area A of the pasture, is equal to the base 120-2x times the height x:
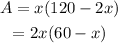
Find the maximum value of the 2nd degree polynomial for A. Since A has roots at x=0 and x=60, the maximum value is found at x=(60+0)/2=30.
Then, the maximum possible area of the pasture can be found by plugging in x