We can think of a hexagon in the next way:
This is, a shape made of 6 smaller triangles. So, we only need to calculate the area of one of those triangles and multiply it by 6
There is something interesting, each of the angles of every one of the triangles is 60°, those are equilateral triangles. So, let's focus on one triangle:
Notice that the blue line is the height of the triangle, that's what we need to find it's are using the formula:
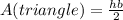
So, to calculate the height we use the Pythagoras Theorem
![H^2-O^2=b^2\Rightarrow(20\operatorname{cm})^2-10\operatorname{cm}=b^2\Rightarrow b^2=300\operatorname{cm}\Rightarrow b=10\sqrt[]{3}]()
Finally, the area of one of the triangles is:
![A(triangle)=(1)/(2)(20cm)(10\sqrt[]{3}cm)=173.2cm^2](https://img.qammunity.org/2023/formulas/mathematics/college/du7nvajn984lqcl3cldtj3v1po5az85qdv.png)
And, by multiplying the previous result by 6, we get the area
![A(hexagon)=6\cdot A(triangle)=6(173.2cm^2)=1039.2\operatorname{cm}]()