Question

Suppose that 73% of the residents in a particular community speak English as their primary language.a. What is the probability that exactly seven out of eight random residents in this community will speak English as their primary language?

Answer 1

Step-by-step explanation

The question can be solved using the probability distribution formula, which can be seen below.

`P_x=nCxp^xq^(n-r)`

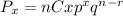
Part A

From the image we can see that n=8 and p=0.73 while q= 1-0.73 = 0.27

Therefore for;

`\begin{gathered} P(7)=8C7(0.73)^7(0.27)^1 \\ =(8!)/(7!1!)*(0.73)^7(0.27)^1 \\ =0.23862 \end{gathered}`

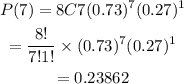
Answer: 0.2386

Part B

`\begin{gathered} Pr(x\ge7)=Pr(7)+Pr(8)=8C7(0.73)^7(0.27)^1+8C8(0.73)^8(0.27)^0 \\ =(8!)/(7!1!)*(0.73)^7(0.27)^1+(8!)/(8!0!)*(0.73)^8(0.27)^0 \\ =0.23862+0.08064 \\ =0.31926 \end{gathered}`

Answer: 0.3193

Part C: Out of a random number of 40 people in the community, the expected number of people that speak English as a lnaguage will be;

`(73)/(100)*40=29.20`

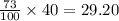
Answer: 29.20