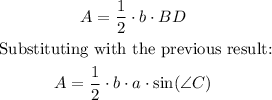Sine formula

Considering angle C from triangle BCD, the opposite side is side BD and the hypotenuse is side BC which length is a units. Then:

The area of a triangle is calculated as follows:
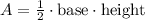
In triangle ABC the base is b units long and its height is segment BD, then the area of triangle ABC is: