Answer:
m>60
Explanation:
Let the number of miles driven = m
Company A charges $97 and allows unlimited mileage.
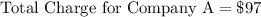
Company B has an initial fee of $55 and charges an additional $0.70 for every mile driven.
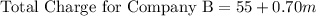
When the charge for Company A is less than that of Company B:
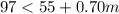
We then solve the inequality for m:

Company A will charge less than Company B when the number of miles driven, m is greater than 60.