Question

Our galaxy, the Milky Way, contains approximately 4.0 x 1011 stars with anaverage mass of 2.0 X 1030 kg each. How far away is the Milky Way from ournearest neighbor, the Andromeda Galaxy, if Andromeda contains roughly thesame number of stars and attracts the Milky Way with a gravitational force of2.4 x 1030 N?

Answer 1

We will have the following:

First, we remember:

`F=(Gm_1m_2)/(r^2)`

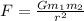
Then, from the problem we will have that:

`2.4\ast10^(30)N=(G(2.0\ast10^(30)kg)(2.0\ast10^(30)kg))/(r^2)`
`\Rightarrow r^2=(G(2.0\ast10^(30)kg)^2)/(2.4\ast10^(30)N)\Rightarrow r\approx1.1116666667\ast10^(20)m`

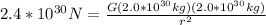
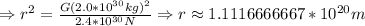
So, the Andromeda galaxy is approximately 1.1*10^20 meters from the milky way.

The acceleration of the Andromeda galaxy towards the milky way is:

`2.4\ast10^(30)N=(2.0\ast10^(30)kg)a\Rightarrow a=1.2m/s^2`

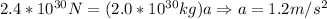
So, the acceleration towards the milky ways is 1.2m/s^2.