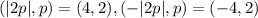Solution
We have the following equation:
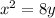
the general formula for a parabola is given by:
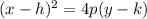
Where (h,k) =(0,0) represent the vertex, so then our equation is:
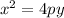
By direct comparison we have this:
4p= 8
p = 2
Then the focus is given by:
(0,p) = (0,2)
the directrix is given by:
y= 0-p = 0-2= -2
y=-2
And finally the 2 focal chord endpoints are: