We will determine if the sets are proportional, if they are, then those will be the sets of lengths that would belong to triangle z, that is:
a.
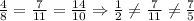
So, set a is not one.
b.
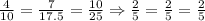
So, set b could be a set of lengths that belong to triangle z.
c.
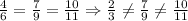
So, set c is not one.
d.
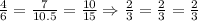
So, set d could be a set of lengths that belong to triangle z.
e.
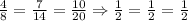
So, set e could be a set of lengths that beling to triangle z.
So, the options that could be candidate are: b, d & e.