Question

Use the Pythagorean theorem to find the length of this segment.

Answer 1

To find the length of the segment use the Pythagoras theorem below:

`AC^2=AB^2+BC^2`

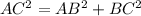
From the graph, we have:

AB = 15 - 3 = 12

BC = 7 - 2 = 5

Let's solve for the length of the segment AC:

`\begin{gathered} AC^2=12^2+5^2 \\ \\ AC^2=144+25 \\ \\ AC^2=169 \end{gathered}`

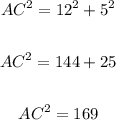
Take the square-root of both sides:

`\begin{gathered} \sqrt[]{AC^2}=\sqrt[]{169} \\ \\ AC\text{ = 13} \end{gathered}`

Therefore, the length of this segment is 13

ANSWER:

13