Question

A model rocket is launched with an initial upward velocity of 215 ft/s. The rockets height h in feet) after t seconds is given by the following.h=215t-16t^2Find all values for t for which the rockets height is 97 feet.Round your answer(s) to the nearest hundredth.

Answer 1

Given,

The initial velocity of the rocket, u=215 ft/s

The equation which gives the height of the rocket at any given instant of time,

`h=215t-16t^2`

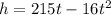
The height of the rocket, h=97 ft.

The given equation is a quadratic equation. On rearranging the above equation and substituting the value of h,

`\begin{gathered} 16t^2-215t+h=0 \\ 16t^2-t+97=0 \end{gathered}`

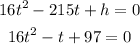
A quadratic equation is written as,

`ax^2+bx+c=0`

Comparing the two equations,

x=t, a=16, b=-215, c=97.

The solution of a quadratic equation is given by,

`x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

On substituting the known values in the above equation,

`\begin{gathered} t=\frac{-(-215)\pm\sqrt[]{(-215)^2-4*16*97}}{2*16} \\ =\frac{215\pm\sqrt[]{40017}}{32} \\ =12.97\text{ or}\pm0.47\text{ } \end{gathered}`

Thus, the values of t are 12.97 s or 0.47 s.

That is, the rocket will be at a height of 97 feet at t=12.97 s or t=0.47 s